Q.
A bob of mass $m$ is suspended by a light string of length $L$. It is imparted a horizontal velocity $v_{0}$ at the lowest point $A$ such that it completes a semi-circular trajectory in the vertical plane. The string becomes slack only on reaching the topmost point $C$ as shown in figure. Then, the speed of bob $\left(v_{0}\right)$ at point $A$ is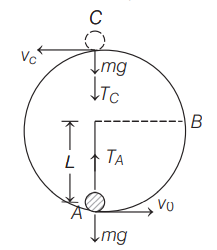
Work, Energy and Power
Solution: