Q.
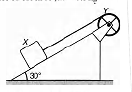
A block X of mass 0.5 kg is held by a long massless string on a frictionless inclined plane of inclination 30$^{\circ}$ to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass 2 kg and of radius 0.2 mas shown in figure.
The drum is given an initial angular velocity such that the block X starts moving up the plane.
(a) Find the tension in the string during the motion.
(b) At a certain instant of time the magnitude of the angular velocity o ff is $10 rads^{-1}$. Calculate the distance travelled by X from that instant of time until it comes to rest.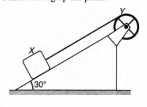
IIT JEEIIT JEE 1994System of Particles and Rotational Motion
Solution:
Given, mass of block X , m= 0.5kg
Mass of drum Y, M = 2kg
Radius of drum, R = 0.2 m
Angle of inclined plane, $\theta=30^{\circ}$
(a) Let a be the linear retardation of block X and $\alpha$ be the angular retardation of drum Y. Then,
$a=R\alpha$
$mg sin 30^{\circ}-T=ma$...(i)
or $\frac{mg}{2}-T=ma$...(ii)
$\alpha=\frac{\tau}{I}=\frac{TR}{\frac{1}{2}MR^2}$
or $\alpha=\frac{2T}{MR}$....(iii)
Solving Eqs. (i), (ii) and (iii) for T, we get,
$T=\frac{1}{2}\frac{M mg}{M+2m}$
Substituting the value we get,
$T=\bigg(\frac{1}{2}\bigg)\biggl\{\frac{(2)(0.5)(9.8)}{2+(0.5)(2)}\biggl\}$
$=1.63N$
(b) From Eq. (iii), angular retardation of drum
$\alpha=\frac{2T}{MR}=\frac{(2)(1.63)}{(2)(0.2)}=8.15 rad/s^2$
or linear retardation of block
$a=R\alpha=(0.2)(8.15)=1.63 m/s^2$
At the moment when angular velocity of drum is
$\omega_0=10rad/s$
The linear velocity of block will be
$v_0=\omega_0R=(10)(0.2)=2m/s$
Now, the distance (s) travelled by the block until it comes to rest will be given by
$s=\frac{v^2_0}{2a}$ $(Using v^2 = V^2_0-2as with v = 0)$
$=\frac{(2)^2}{2(1.63)}$
or $s=1.22m$