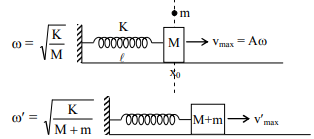
Question

A block with mass $M$ is connected by a massless spring with stiffness constant $k$ to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position $x _{0}$. Consider two cases : (i) when the block is at $x _{0}$; and (ii) when the block is at $x = x _{0}+ A$. In both the cases, a particle with mass $m (< M )$ is softly placed on the block after which they stick to each other. Which of the following statement(s) is(are) true about the motion after the mass $m$ is placed on the mass $M$ ?

• A. The amplitude of oscillation in the first case changes by a factor of $\sqrt{\frac{M}{m+M}}$, whereas in the second case it remains unchanged
• B. The final time period of oscillation in both the cases is same
• C. The total energy decreases in both the cases
• D. The instantaneous speed at $x _{0}$ of the combined masses decreases in both the cases

Answer 1

Answer: (A), (B), (D)

$MA \omega=( m + M ) A' \omega'$
$A'=\frac{ M }{ m + M } \frac{\omega}{\omega'} A$
$A'=\frac{ M }{ m + M } \cdot \sqrt{\left(\frac{ M + m }{ M }\right) A }$
$A'=\sqrt{\frac{ M }{ m + M }} A$
Amplitude in $I ^{ st }$ Changes by a factor of $\sqrt{\frac{ M }{ m + M }}$
Time period of $I^{s t}$ case $=2 \pi \sqrt{\frac{m+M}{K}}$

Amplitude remain same.
But time period because $=2 \pi \sqrt{\frac{ m + M }{ K }}$
Total energy of $I ^{\text {st }}$ case decreases due to decrease in amplitude. Instantaneous speed in $I ^{\text {st }}$ case decrease
In $II ^{ nd }$ case $\frac{1}{2} KA ^{2}=\frac{1}{2}( m + M ) v ^{\prime 2}$
So also decrease.