Q.
A block rests on a fixed wedge inclined at an angle $\theta$. The coefficient of friction between the block and plane is $\mu$. The maximum value of $\theta$ for the block to remain motionless on the wedge is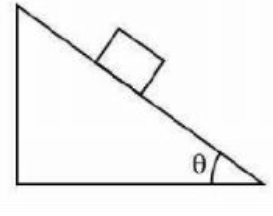
TS EAMCET 2020
Solution:
