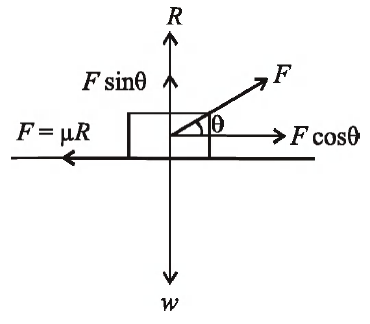
Q. A block of weight $W$ rests on a horizontal floor with coefficient of static friction $\mu$. It is desired to make the block move by applying minimum amount of force. The angle $\theta$ from the horizontal at which the force should be applied and magnitude of the force $F$ are respectively.
AIEEEAIEEE 2012Laws of Motion
Solution:
Let the force $F$ is applied at an angle $\theta$ with the horizontal.
For horizontal equilibrium,
$F\,cos\,\theta=\mu R\,...\left(i\right)$
For vertical equilibrium,
$R + F\, sin\,\theta = mg$
or, $R=mg-F\,sin\theta \,...\left(ii\right)$
Substituting this value of $R$ in eq. $\left(i\right), $we get
$F\,cos\,\theta =\mu\left(mg-F\,sin\theta\right)$
$=\mu\,mg-\mu\,Fsin\theta$
or, $F\left(cos\theta+\mu sin\theta\right)=\mu mg$
or, $F=\frac{\mu mg}{cos\theta +\mu sin\theta }\, ...\left(iii\right)$
For $F$ to be minimum, the denominator
$\left(cos\theta +\mu sin\theta \right)$ should be maximum.
$\therefore \frac{d}{d\theta}\left(cos\theta +\mu sin\theta \right)=0$
or, $-sin\theta +\mu sin\theta =0$
or, $tan\theta +\mu$
or, $\theta=tan^{-1}\left(\mu\right)$
Then, $sin\theta=\frac{\mu}{\sqrt{1+\mu^{2}}}$ and
$cos\,\theta=\frac{1}{\sqrt{1+\mu^{2}}}$
Hence, $F_{min} =\frac{\mu w}{\frac{1}{\sqrt{1+\mu^{2}}}+\frac{\mu^{2}}{\sqrt{1+\mu^{2}}}}=\frac{\mu w}{\sqrt{1+\mu^{2}}}$