Question

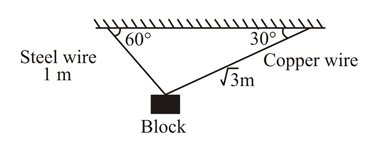
A block of weight $100\,N$ is suspended by copper and steel wires of same cross sectional area $0.5\,cm^{2}$ and, length $\sqrt{3}\,m$ and $1\,m,$ respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are $30^\circ $ and $60^\circ ,$ respectively. If elongation in copper wire is $\left(\Delta I_{c}\right)$ and elongation in steel wire is $\left(\Delta I_{s}\right),$ then the ratio $\frac{\Delta I_{C}}{\Delta l_{S}}$ is [Young's modulus for copper and steel are $1\times 10^{11}N/m^{2}$ and $2\times 10^{11}N/m^{2},$ respectively]

Answer 1

$\frac{T_{s}}{2}=T_{c}\frac{\sqrt{3}}{2}$
$T_{s}=\sqrt{3}T_{c}$
$\frac{\Delta \ell _{c}}{\Delta \ell _{s}}=\left(\frac{T_{c}}{T_{s}}\right)\left(\frac{\ell _{C}}{\ell _{S}}\right)\left(\frac{Y_{S}}{Y_{C}}\right)=\left(\frac{1}{\sqrt{3}}\right)\left(\frac{\sqrt{3}}{1}\right)\left(\frac{2 \times \left(10\right)^{11}}{1 \times \left(10\right)^{11}}\right)=2$