Question

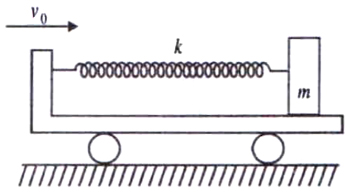
A block of mass $m$ is connected rigidly with a smooth wedge (plank) by a light spring of stiffness $k$. If the wedge is moved with constant velocity $v_0$, then find the work done by the external agent until the maximum compression of the spring.

• A. $m{v}_0^2$
• B. $2m{v}_0^2$
• C. $3m{v}_0^2$
• D. $2m{v}_0^3$

Answer 1

Answer: (A)

Let us take wedge + spring + block as a system. The forces responsible for performing work are spring force $k x(\leftarrow)$ and the external force $F (\rightarrow)$.

Work Energy theorem for block $+$ spring $+$ plank relative to ground:
Applying work-energy theorem, we have $W_{\text {ext }}+W_{\text {sp }}=\Delta K$ where $W_{s p}$ the total work done by the spring on wedge and block $-\frac{1}{2} k x^{2}$ and $\Delta K =$ change in $KE$ of the block (because the plank does not change its kinetic energy)
Then, $\quad W_{\text {ext }}=\frac{1}{2} k x^{2}+\Delta K$
As the block was initially stationary and it will acquire a velocity $v _{0}$ equal to that of the plank at the time of maximum compression of the spring, the change in kinetic energy of the block relative to ground is
$\Delta K =\frac{1}{2} m v_{0}^{2}$
Substituting $\Delta K$ in the above equation, we have
$W _{\text {ext }}=\frac{1}{2} K x^{2}+\frac{1}{2} m v_{0}^{2} \quad \ldots( i )$
Work Energy theorem for block + spring + plank relative to the plank $W_{\text {ext }}+W_{\text {sp }}=\Delta K$ The plank moves with constant velocity, there is no pseudo-force acting on the block. Wext $=0$ Then the net work done on the system (block + plank), due to the spring, can be given as
$W _{ SP }=-\frac{1}{2} k x^{2}$
As the relative velocity between the observer (plank) and block decreases from $v_{0}$ to zero at the time of maximum compression of the spring, the change in kinetic energy of the block is $\Delta K =-\frac{1}{2} m v_{0}^{2} .$
Substituting $W _{ sp }$ and $\triangle K$ in above equation $-\frac{1}{2} k x^{2}=-\frac{1}{2} m v_{0}^{2}$ (ii)
From (i) & (ii)
$W _{\text {ext }}=\frac{1}{2} m v_{0}^{2}+\frac{1}{2} m v_{0}^{2}=m v_{0}^{2}$