Question

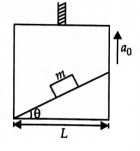
A block of mass $m$ starting from rest slides down a smooth inclined plane of gradient $\theta$, fixed in a lift moving upwards with an acceleration $a_{0}$ as shown in figure. If the base of the inclined plane has length $L$, the time taken by the block to slide from top to bottom of the inclined plane, will be

• A. $\frac{L}{\left(g+a_{0}\right) \sin 2 \theta}$
• B. $\left[\frac{4 L}{\left(g+a_{0}\right) \sin 2 \theta}\right]^{1 / 2}$
• C. $\frac{\left(g+a_{0}\right) \sin 2 \theta}{2 L}$
• D. $\left[\frac{2 L}{\left(g+a_{0}\right) \sin \theta}\right]^{2}$

Answer 1

Answer: (B)

Acceleration along the inclined plane,
$a=\left(g+a_{0}\right) \sin \theta$
Slope length $=\frac{L}{\cos \theta}$
Using $s=u t+\frac{1}{2} a t^{2},$ weget $\frac{L}{\cos \theta}=0 \times t+\frac{1}{2}\left(g+a_{0}\right) \sin \theta t^{2}$
or $t=\sqrt{\frac{2 L}{\left(g+a_{0}\right) \sin \theta \cos \theta}}$ or $t=\sqrt{\frac{4 L}{\left(g+a_{0}\right) \sin 2 \theta}}$