Question

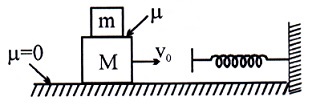
A block of mass $M$ slides on a frictionless surface with an initial speed of $v_{0}$ . On top of the block, there is a small block of mass $m$ . The coefficient of friction between the blocks is $\mu $ . The system of blocks encounters an ideal spring with force constant $k$ . The maximum value of $k$ for which the blocks don't slip relative to each other is

• A. $\left(\frac{\mu g}{v_{0}}\right)^{2}\frac{\left(m + M\right)^{2}}{m}$
• B. $\left(\frac{\mu g}{v_{0}}\right)^{2}\left(m + M\right)$
• C. $\left(\frac{\mu g}{v_{0}}\right)^{2}\frac{\left(m + M\right)^{2}}{M}$
• D. $\left(\frac{\mu g}{v_{0}}\right)^{2}\left(M - m\right)$

Answer 1

Answer: (B)

$\frac{1}{2}\left(M + m\right)\left(v_{0}\right)^{2}=\frac{1}{2}kx^{2}$
$x=v_{0}\sqrt{\frac{M + m}{k}}$
Also for the upper block
$f_{m a x}=\mu mg=m\frac{k}{m + M}x$
$\mu g=\frac{k}{m + M}\left(v_{0} \sqrt{\frac{m + M}{k}}\right)$
$\Rightarrow \frac{k}{m + M}=\left(\frac{\mu g}{v_{0}}\right)^{2}$
$\Rightarrow k=\left(\frac{\mu g}{v_{0}}\right)^{2}\left(m + M\right)$