Question

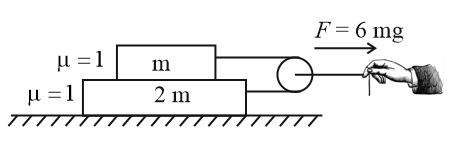
A block of mass $m$ sits on the top of a block of mass $2m$ which sits on a table. The coefficient of kinetic friction between all surface is $\mu \, = \, 1$ . A massless string is connected to each mass and wraps halfway around a massless pulley, as shown. Assume that you pull on the pulley with a force of $6mg$ . The acceleration of your hand is -

• A. $\frac{g}{2}$
• B. $2g$
• C. $\frac{5 g}{4}$
• D. $\frac{4 g}{5}$

Answer 1

Answer: (C)

The free body diagrams are :

$F_{1}$ is force of friction between blocks
$F_{2}$ is force of friction between block and ground
Making FBD of pulley

Since pulley is light
$T=\frac{F}{2}=3mg$
Let blocks move together with common acceleration a
$a=\frac{6 m g - F_{2}}{3 m}=\frac{6 m g - 3 m g}{3 m}=g$
then for upper block
$T-F_{1}=ma\Rightarrow 3mg-F_{1}=mg\Rightarrow F_{1}=2mg$
but $F_{1}$ should be less than $f_{max}=\mu mg$
So, our assumption of no relative motion b/w blocks is incorrect that means there is relative motion
$\Rightarrow \, \, F_{1}$ is kinetic $=\mu mg$
$a_{m}=\frac{3 m g - \mu m g}{m}2g\left(t o w a r d \, s r i g h t\right)$
$a_{2 m}=\frac{3 m g + \mu m g - 3 \mu m g}{2 m}=\frac{g}{2}\left(t o w a r d \, s r i g h t\right)$
acceleration of pulley = accelerated of hand
$a_{p}=\frac{a_{m} + a_{2 m}}{2}=\frac{2 g + \frac{g}{2}}{2}=\frac{5 g}{4}\left(t o w a r d \, s r i g h t\right)$