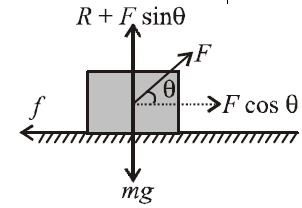
Q. A block of mass $m$ is pulled along a horizontal surface by applying a force at an angle $\theta$ with the horizontal. If the block travels with a uniform velocity and has a displacement $d$ and the coefficient of friction is $\mu$ then the work done by the applied force is
Solution:
Because the block moves with a uniform velocity, the resultant force is zero. Resolving $F$ into horizontal component $F \,\cos \,\theta$ and vertical component $F \,\sin \,\theta$, we get
$R + F \,sin \,\theta = mg$ or $R = mg - F \,\sin\,\theta$
Also $f = μR = μ(mg - F \,sin \,\theta)$
But $F\,cos\,\theta = f$
or $F\,\cos\,\theta = μ(mg - F\,\sin\,\theta)$
or $F(\cos \,\theta + μ \,sin \,\theta) = μmg$
$\therefore F=\frac{\mu\, mg}{\cos\, \,\theta + \mu \,sin\, \theta}$
Work $W = Fs \,cos\,\theta$
$\therefore W=\frac{\mu \,mgd \,\cos \,\theta}{\cos\, \theta + \mu \,sin\, \theta}$
$\left(\because s=d\right)$