Question

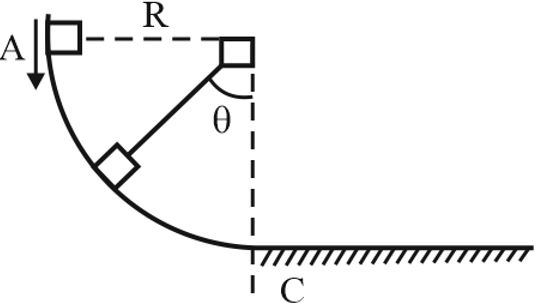
A block of mass $m$ is placed on a vertical fixed circular track and then it is given velocity $v$ along the track at position $A$ on track. The coefficient of friction between the block and the track varies with the angle $\theta $ . If the block moves on track with constant speed then the coefficient of friction is

• A. $\mu =\frac{sin \theta }{cot ⁡ \theta + \frac{v^{2}}{R g}}$
• B. $\mu =\frac{sin \theta }{cos ⁡ \theta + \frac{v^{2}}{R g}}$
• C. $\mu =\frac{tan \theta }{c o s \theta + \frac{v^{2}}{R \, g}}$
• D. $\mu =\frac{cos \theta }{tan \theta + \frac{v^{2}}{R \, g}}$

Answer 1

Answer: (B)

Since the block is moving with a constant speed, at any instant its tangential acceleration is zero. Hence,
$f=mgsin\theta $
Also,
$N-mgcos\theta =\frac{m v^{2}}{R}$
$N=\frac{m v^{2}}{R}+mgcos\theta $
$f=\mu N=\mu \frac{m v^{2}}{R}+\mu mgcos\theta $
$mgsin\theta =\mu \frac{m v^{2}}{R}+\mu mgcos\theta $
$\Rightarrow \mu =\frac{s i n \theta }{c o s \theta + \frac{v^{2}}{R \, g}}$