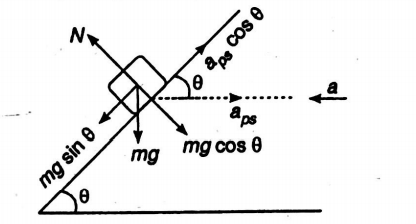
Question

A block of mass $m$ is placed on a smooth wedge of inclination $9$. The whole system is accelerated horizontally so that the block does not slip on the wedge. The force exerted by the wedge on the block ($g$ is acceleration due to gravity) will be

• A. $ mg\,cos\theta $
• B. $ mg\,\sin \,\theta $
• C. $ mg $
• D. $ mg/cos\,\theta $

Answer 1

Answer: (D)

Let an acceleration to the wedge is given towards left, then the block (being in non-inertial frame) has a pseudo acceleration to the right because of which the block is not slipping
$ \therefore $ $ mg\sin \theta ={{a}_{pesudo}}\cos \theta $
$ \Rightarrow $ $ {{a}_{pseudo}}=\frac{mg\sin \theta }{\cos \theta } $
Hence, total force exerted by the wedge on the block is
$ N={{N}_{1}}+{{N}_{2}} $

$ =mg\cos \theta +{{q}_{pseudo}}\sin \theta $
$ =mg\cos \theta +\frac{mg\sin \theta }{\cos \theta }\times \sin \theta $
$ =\frac{mg{{\cos }^{2}}\theta +mg{{\sin }^{2}}\theta }{\cos \theta }=\frac{mg}{\cos \theta } $
If the block is not given a horizontal acceleration ie the block is permanently at rest, the net force on it will be zero. Thus. in this case force exerted by the wedge on the block is mg (upwards).