Question

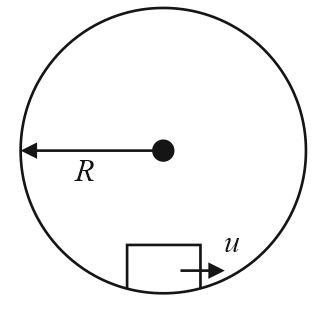
A block of mass $m$ is placed at the lowest point of a smooth vertical track of radius $R$ . In this position, the block is given a horizontal velocity $u$ such that the block is just able to perform a complete vertical circular motion. The acceleration of block, when its velocity is vertical is

• A. $g$
• B. $3g$
• C. $g\sqrt{10}$
• D. $2\sqrt{2}g$

Answer 1

Answer: (C)

The initial velocity of the block to undergo a complete vertical circular motion is $u=\sqrt{5 g R}$

Let us assume that the speed of the block when it is moving in the vertical direction is $v$ , then using conservation of mechanical energy we get
$\frac{1}{2}m\left(\sqrt{5 g R}\right)^{2}=\frac{1}{2}mv^{2}+mgR$
$\Rightarrow v^{2}=\sqrt{3 g R}$
The tangential and centripetal accelerations of the block are
$a_{t}=g\left(\downarrow\right)$ and $a_{c}=3g\left(\leftarrow\right)$
$a_{net}=\sqrt{a_{c}^{2} + a_{t}^{2}}=g\sqrt{10}$