Q.
$A$ block of mass $m$ is on an inclined plane of angle $\theta$. The coefficient of friction between the block and the plane is $\mu$ and tan $\theta >\mu.$ The block is held stationary by applying a force $P$ parallel to the plane. The direction of force pointing up the plane is taken to be positive. As $P$ is varied from $P_{1}=mg$ $\left(\sin\,\theta-\mu\,\cos\,\theta\right)$ to $P_{2}=mg\left(\sin\theta+\mu \cos\theta\right)$, the frictional force $f$ versus $P$ graph will look like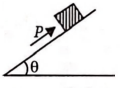
IIT JEEIIT JEE 2010Laws of Motion
Solution: