Question

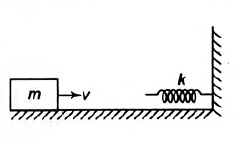
A block of mass m is moving with a speed $v$ on a horizontal rough surface and collides with a horizontally mounted spring of spring constant $k$ as shown in the figure. The coefficient of friction between the block and the floor is $\mu$ The maximum compression of the spring is

• A. $-\frac{\mu \text{mg}}{k}+\frac{1}{k}\sqrt{\left(\mu \text{mg}\right)^{2}+mkv^{2}}$
• B. $\frac{\mu \text{mg}}{k}+\frac{1}{k}\sqrt{\left(\mu \text{mg}\right)^{2}+mkv^{2}}$
• C. $-\frac{\mu \text{mg}}{k}-\frac{1}{k}\sqrt{\left(\mu \text{mg}\right)^{2}-mkv^{2}}$
• D. $\frac{\mu \text{mg}}{k} - \frac{1}{k}\sqrt{\left(\mu \text{mg}\right)^{2}+mkv^{2}}$

Answer 1

Answer: (A)

In presence of friction, both the spring force and the frictional act so as to oppose the compression of the spring.
Work done by the net force
$W=-\frac{1}{2} k x_{m}^{2}-\mu m g x_{m}$
where $x_{m}$ is the maximum compression of the spring.
Change in kinetic energy
$\Delta K=K_{f}-K_{i}=0-\frac{1}{2} m v^{2}$
According to work-energy theorem
$W= \Delta K$
$-\frac{1}{2} k x_{m}^{2}-\mu m g x_{m}=-\frac{1}{2} m v^{2}$
$k x_{m}^{2}+\mu m g x_{m}=\frac{1}{2} m v^{2}$
$k x_{m}^{2}+2 \mu m g x_{m}-m v^{2}=0$
$x_{m}^{2}+\frac{2 \mu m g x_{m}}{k}-\frac{m v^{2}}{k}=0$
It is a quadratic equation in $x_{m}$.
Solving this quadratic equation for $x_{m}$
and taking only the positive root since $x_{m}$ is positive,
we get
$x_{m}=-\frac{\mu m g}{k}+\frac{1}{k} \sqrt{(\mu m g)^{2}+m k v^{2}}$