Q.
A block of mass $m$ is attached to two unstretched springs of spring constants $k_{1}$ and $k_{2}$ as shown in figure.The block is displaced towards right through a distance $x$ and is released. The speed of the block as it passes through the mean position is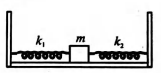
Work, Energy and Power
Solution: