Q.
A block of mass $M$ has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at $x\, = \,0$ in a co-ordinate system fixed to the table. A point mass m is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is $x$ and the velocity is $v$. At that instant, which of the following options is/are correct?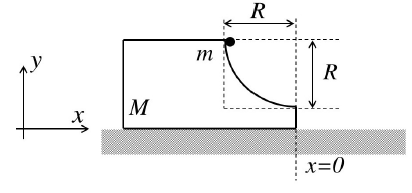
Solution:
