Q.
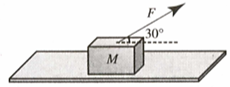
A block of mass, $M=5kg$ is resting on a rough horizontal surface for which the coefficient of friction is $0.2$ . Let a force, $F=40N$ be applied, what will then the acceleration of the block be?
NTA AbhyasNTA Abhyas 2022
Solution:
FBD of the block is shown below
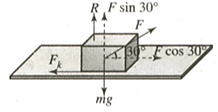
Kinetic friction acting on the body $=\left(\mu \right)_{k}R=0.2\left(M g - F sin \left(30\right)^{o}\right)$
$=0.2\left(5 \times 10 - 40 \times \frac{1}{2}\right)=0.2\left(50 - 20\right)=6 \, N$
By Newton's second law of motion, acceleration of the block
$=\frac{netforce}{m a s s}$ $=\frac{F cos 30^{o} - k i n e t i c \, f r i c t i o n}{m a s s}$ $=\frac{40 \times \frac{\sqrt{3}}{2} - 6}{5}=5.73 \, m/s^{2}$

Kinetic friction acting on the body $=\left(\mu \right)_{k}R=0.2\left(M g - F sin \left(30\right)^{o}\right)$
$=0.2\left(5 \times 10 - 40 \times \frac{1}{2}\right)=0.2\left(50 - 20\right)=6 \, N$
$=\frac{netforce}{m a s s}$ $=\frac{F cos 30^{o} - k i n e t i c \, f r i c t i o n}{m a s s}$ $=\frac{40 \times \frac{\sqrt{3}}{2} - 6}{5}=5.73 \, m/s^{2}$