Q.
A block of mass $m=25\, kg$ sliding on a smooth horizontal surface with a velocity $v=3\, ms ^{-1}$ meets the spring of spring constant $k=100\, N / m$ fixed at one end as shown in figure. The maximum compression of the spring and velocity of block as it returns to the original position respectively are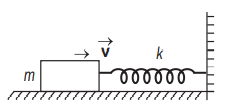
EAMCETEAMCET 2007Work, Energy and Power
Solution: