Question

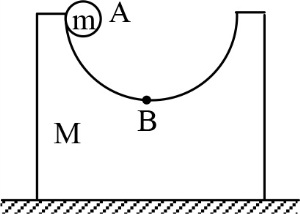
A block of mass $M=2 \, kg$ with a semicircular track of radius $R=1.1 \, m$ rests on a horizontal frictionless surface. A uniform cylinder of radius $r=10 \, cm$ and mass $m=1.0 \, kg$ is released from rest from the top point $A$ . The cylinder slips on the semicircular frictionless track. The speed of the block when the cylinder reaches the bottom of the track at $B$ is $\left(g = 10 \, m \, s^{- 2}\right)$

• A. $\sqrt{\frac{10}{3 \, }} \, m \, s^{- 1}$
• B. $\sqrt{\frac{4}{3}}ms^{- 1}$
• C. $\sqrt{\frac{5}{2}}ms^{- 1}$
• D. $\sqrt{10}ms^{- 1}$

Answer 1

Answer: (A)

Let the speed of the block be $v$ . Then from conservation of momentum, the velocity of the cylinder will be $2v$ in the opposite direction $\left(m = \frac{M}{2}\right)$
Now from conservation of energy
$mgh=\frac{1}{2}Mv^{2}+\frac{1}{2}m\left(2 v\right)^{2}, \, h=R-r=1 \, m$
so $v=\sqrt{\frac{10}{3 \, }} \, m \, s^{- 1}$