Q.
A block of mass $m=2\, Kg$ is initially at rest oil a horizontal surface. A horizontal force $\vec{F}_{1}=(6\,N ) \hat{i}$ and a vertical force $\vec{ F _{2}}=(10 \,N ) \hat{j}$ are then applied to the block. The coefficients of static friction and kinetic friction for the block and the surface are $0.4$ and $0.25$ respectively. The magnitude of the frictional force acting on the block is
(Assume $g =10\, m / s ^{2}$ )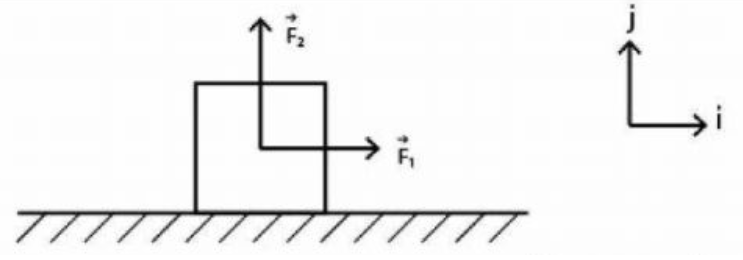
TS EAMCET 2020
Solution:
