Question

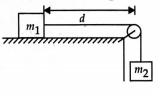
A block of mass $m_{1}$ lies on a smooth horizontal table and is connected to another freely hanging block of mass $m_{2}$ by a light inextensible string passing over a smooth fixed pulley situated at the edge of the table as shown in the figure. Initially the system is at rest with $m_{1}$ at a distance $d$ from the pulley. The time taken for $m_{1}$ to reach the pulley is

• A. $\frac{m_{2} g}{m_{1}+m_{2}}$
• B. $\sqrt{\frac{2 d\left(m_{1}+m_{2}\right)}{m_{2} g}}$
• C. $\sqrt{\frac{2 m_{2} d}{\left(m_{1}+m_{2}\right) g}}$
• D. $\sqrt{\frac{2 m_{1} d}{\left(m_{1}+m_{2}\right) g}}$

Answer 1

Answer: (B)

Let $a$ be the common acceleration of the system. The free body diagrams of two blocks are as shown in the figure. Their equations of motion are
$T=m_{1} a \ldots$ (i)
$m_{2} g-T=m_{2} a \,\,\,\,\, ....(i)$
From (i) and (ii), we get
$a=\frac{m_{2} g}{m_{1}+m_{2}} \,\,\,\,\, ....(ii)$
Using, $s=u t+\frac{1}{2} a t^{2}$
$\therefore d=0 \times t+\frac{1}{2} \frac{m_{2} g}{m_{1}+m_{2}} t^{2} \,\,\,\, (Using (iii))$
or $ t=\sqrt{\frac{2 d\left(m_{1}+m_{2}\right)}{m_{2} g}}$