Question

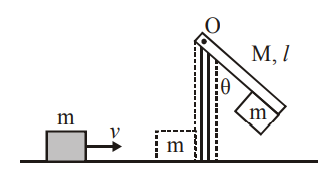
A block of mass $m =1 kg$ slides with velocity $v=6 m / s$ on a frictionless horizontal surface and collides with a uniform vertical rod and sticks to it as shown. The rod is pivoted about $O$ and swings as a result of the collision making angle $\theta$ before momentarily coming to rest. If the rod has mass $M =2 kg ,$ and length $l=1 m ,$ the value of $\theta$ is approximately :
(Take $\left. g =10 m / s ^{2}\right)$

• A. $69^{\circ}$
• B. $63^{\circ}$
• C. $55^{\circ}$
• D. $49^{\circ}$

Answer 1

Answer: (B)

Angular momentum conservation
$mv l=\frac{ M l^{2}}{3} \omega+ m l^{2} \omega$
$\Rightarrow \omega=\frac{1 \times 6 \times 1}{\frac{2}{3}+1}$
$=\frac{18}{5}$
Now using energy consevation
$\frac{1}{2}\left( M \frac{l^{2}}{3}\right) \omega^{2}+\frac{1}{2}\left( m l^{2}\right) \omega^{2}$
$=(m+M) r_{c m}(1-\cos \theta)$
$=( m + M )\left(\frac{ m l+\frac{ M l}{2}}{ m + M }\right) g (1-\cos \theta)$
$\frac{5}{6} \times\left(\frac{18}{5}\right)^{2}=20(1-\cos \theta)$
$\Rightarrow 1-\cos \theta=\frac{18}{5} \times \frac{3}{20}$
$\cos \theta=1-\frac{27}{50}$
$\cos \theta=\frac{23}{50}$
$\Rightarrow \theta \simeq 63^{\circ}$