Q.
A block of mass $m$ is lying on a rough inclined plane having an inclination $\alpha=\tan ^{-1}\left(\frac{1}{5}\right)$. The inclined plane is moving horizontally with a constant acceleration of $a=2\, ms ^{-2}$ as shown in the figure. The minimum value of coefficient of friction, so that the block remains stationary with respect to the inclined plane is (Take, $g=10\, ms ^{-2}$ )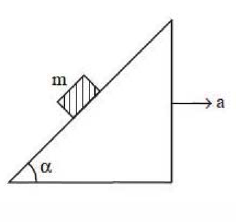
AP EAMCETAP EAMCET 2019
Solution:
