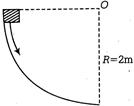
Q. A block of mass $3 \,kg$ starts from rest and slides down a curved path in the shape of a quarter-circle of radius $2\,m $ and reaches the bottom of path with a speed $1\,m/s $ . If $g$ is $ 10\,m/s^{2},$ the amount of work done against friction is
J & K CETJ & K CET 2015Work, Energy and Power
Solution:
Applying Work-Energy theorem, we can write
$\Delta W=\Delta K$
$\Rightarrow W_{t}+W_{g}=K_{t}=K_{i}$
Where. $W_{f}=$ Work done by frictional force
$W_{g}=$ Work done by gravity
$W_{f}=$ Final kinetic energy
$W_{i}=$ Initial kinetic energy
$\Rightarrow W_{f}+m g=\frac{1}{2} m v^{2}-0$
$\Rightarrow W_{f}=\frac{1}{2} m v^{2}-m g R$
$=\frac{1}{2} \times 3 \times 16-3 \times 10 \times 2$
$=24-60=-36\, J$