Q.
A block of mass $\sqrt{3} \,kg$ resting on a horizontal surface. A force $F$ is applied on the block as shown in figure. If coefficient of friction between the block be $\frac{1}{2 \sqrt{3}}$ what can be the maximum value of force $F$ so that block does not start moving? (Take $g=10 \,ms ^{-2}$ )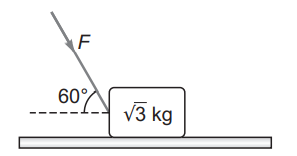
Laws of Motion
Solution:
