Q.
A block of mass $3\, kg$ is pressed against a vertical wall by applying a force, $F$, at an angle $30^{\circ}$ to the horizontal as shown in the figure. As a result, the block is prevented from falling down. If the coefficient of static friction between the block andwall is $\sqrt{3}$, then the value of $F$ is (use $g=10 \,m / s$ )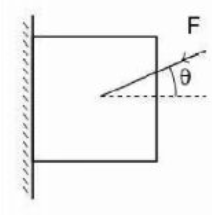
TS EAMCET 2020
Solution:
