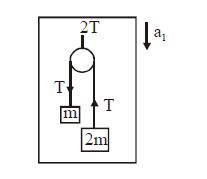
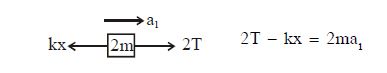Q.
A block of mass 2M is attached to a massless spring with spring-constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1, a2 and a3 as shown in figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0. Which of the following option(s) is/are correct ? [g is the acceleration due to gravity. Neglect friction]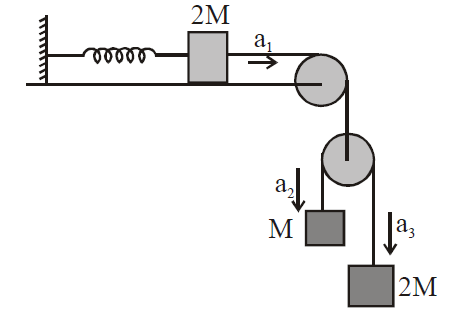
Solution:
$T = \frac{2\left(2m\right)\left(m\right)}{3m}\left(g-a_{1}\right)$
$= \frac{4m}{3}\left(g-a_{1}\right)$
$\frac{8m}{3}\left(g-a_{1}\right)-kx = 2ma_{1}$
$\frac{8Mg}{3}-\frac{8Ma_{1}}{3}-kx = 2ma_{1}$
$\frac{8Mg}{3}-kx = \frac{14ma_{1}}{3}$
$\frac{8Mg-3kx}{14m} = a_{1}$
$a_{1} = \frac{8Mg-3kx}{14m}$
$\frac{vdv}{dx} = \left(\frac{8Mg}{14m}-\frac{3kx}{14m}\right)$
$\int vdv = \frac{1}{14m}\int\left(8Mg-3kx\right)dx$
for max elongation
$0 = \frac{1}{14m} \int\limits^{x_0}_{0}\left(8Mg-3kx\right)dx$
$= \frac{1}{14m}\left(8Mgx_{0}-\frac{3kx^{2}_{0}}{2}\right)$
$8Mgx_{0} = \frac{3kx^{2}_{0}}{2}$
$x_{0} = \frac{16Mg}{3k}$
$at \,x = \frac{x_{0}}{2}$
$\int\limits^{v}_{0} vdv = \frac{1}{14m}\int\limits^{x_0/2}_{0} \left(8Mg-3kx\right)dx$
$\frac{v^{2}}{2} = \frac{1}{14m}\left(\frac{8Mgx_{0}}{2}-\frac{3kx^{2}_{0}}{2\times4}\right)$
$v^{2} = \frac{1}{7m}\left(\frac{8Mg}{2}\times\frac{16Mg}{3x}-\frac{3x}{8}\times\frac{16M^{2}g^{2}}{3x\times3x}\right)$
$= \frac{1}{7m}\left(\frac{64M^{2}g^{2}}{3x}-\frac{2M^{2}g^{2}}{3x}\right)$
$v^{2} = \frac{62Mg^{2}}{21k}$
For acc. $2a_{1} = a_{2} + a_{3}$ therefore
$a_{2} - a_{1} = a_{1} - a_{3}$
$a_{1} = \frac{8Mg-3kx_{0}/4}{14m}$
$= \frac{8g}{14}-\frac{3kx_{0}}{14m\times4}$
$= \frac{8g}{14}-\frac{3x}{14m\times4}\times\frac{16Mg}{3x}$
$= \frac{8g}{14}-\frac{4g}{14}$
$= \frac{4g}{14} = \frac{2g}{7}$
OR
$\frac{8mg}{3}-\frac{8m}{3}a_{1}-kx = 2ma_{1}$
$\frac{14m}{3}a_{1} = -k\left[x-\frac{8mg}{3k}\right]$
$a_{1} = -\frac{3k}{14m}\left[x-\frac{8mg}{3k}\right]....\left(i\right)$
that means, block 2m (connected with the spring) will perform SHM about $x_{1} =\frac{8mg}{3k}$ therefore.
maximum elongation in the spring $x_{0} = 2x_{1} = \frac{16mg}{3k}$
on comparing equation (1) with
$a = \omega^{2}\left(x-x_{0}\right)$
$\omega = \sqrt{\frac{3k}{14m}}$
at $\left(\frac{x_{0}}{2}\right)$, block will be passing through its mean position therefore at mean position
$v_{0} = A\omega = \frac{8mg}{3k} \sqrt{\frac{3k}{14m}}$
At, $\frac{x_{0}}{4}\,\Rightarrow \,x = \frac{A}{2}$
$\therefore \,a_{cc} = -\frac{A}{2} \omega^{2}$
$= -\frac{4mg}{3k}. \frac{3h}{14m} = -\frac{2g}{7}$