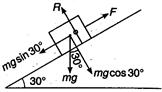
Q. A block of mass $2\,kg $ is lying on an inclined plane, inclined to the horizontal at $30^{\circ} $ . If the coefficient of friction between the block and the plane is $0.7,$ then magnitude of frictional force acting on the block will be
J & K CETJ & K CET 2004
Solution:
The various forces acting on the block are as shown Frictional force
$=\mu R$ ... (i)
where $\mu$ is coefficient of friction and $R$ the normal reaction of the surface on the block.
Also, $R=m g \cos 30^{\circ}$ ... (ii)
From Eqs. (i) and (ii),
we get $F=\mu m g \cos 30^{\circ}$
Given, $\mu=0.7,\, m=2\, kg,\, g=9.8\, m / s^{2}$,
$\cos 30^{\circ}=\frac{\sqrt{3}}{2}$
$\therefore F=0.7 \times 2 \times 9.8 \times \frac{\sqrt{3}}{2}$
$=11.9\, N$