Question

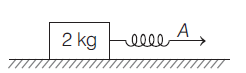
A block of mass $2\, kg$ is connected to an ideal spring and is placed on a smooth horizontal surface. The spring is pulled to move the block and at an instant, the speed of end $A$ of the spring and speed of the block were measured to be $6\, m / s$ and $3 \,m / s$, respectively. At this moment the potential energy stored in the spring in increasing at a rate $15\, J / s$. Find the acceleration of the block at this instant.

• A. $1.5 \,m / s ^{2}$
• B. $3.0 \,m / s ^{2}$
• C. $4.5 \,m / s ^{2}$
• D. $2.5 \,m / s ^{2}$

Answer 1

Answer: (A)

Given, mass of block, $m=2 \,kg$
Since, block is pulled by spring at an instant,
velocity of spring's end, $v_{1}=6 \,m / s$
and velocity of block end, $v_{2}=3\, m / s$
The rate of potential energy,
$\frac{\Delta U}{\Delta t} =\frac{\frac{1}{2} m\left(v_{2}^{2}-v_{1}^{2}\right)}{t} $
$15 =\frac{1}{2} \times 2 \frac{\left(v_{2}+v_{1}\right)\left(v_{2}-v_{1}\right)}{t} $
$\frac{15}{v_{2}+v_{1}} =\frac{v_{2}-v_{1}}{t} $
Now, acceleration $ a=\frac{15}{6+3} $
$a=\frac{15}{9} $
$a= 1.6 \,m / s ^{2} $
$\simeq 1.5 \,m / s ^{2}$