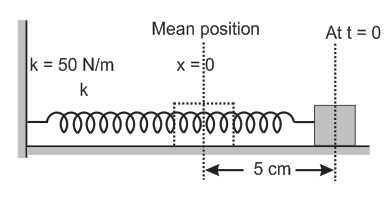
Question

A block of mass $2 \, kg$ is attached to the spring of spring constant $50 \, N/m$ . The block is pulled to a distance of $5 \, cm$ from its equilibrium position $\left(\text{at } x = 0\right)$ on a horizontal frictionless surface and released at $t=0$ from rest. The expression for its displacement at anytime $t$ is

• A. $5sin\left(5 t + \pi / 2\right)$
• B. $sin\left(5 t + \pi / 2\right)$
• C. $5sin\left(5 t + 3 \pi / 2\right)$
• D. $5sin\left(t + \pi / 2\right)$

Answer 1

Answer: (A)

The spring -block system will perform SHM about the mean position with an amplitude $5cm$ .

Given, spring constant $k=50 \, N/m$
m = mass attached = 2 kg
$\therefore \text{Angular frequency} \omega = \sqrt{\frac{k}{m }} = \sqrt{\frac{5 0}{2}} = \sqrt{2 5} = 5 \text{rad/s}$
Assuming the displacement function
y(t) = A sin (ωt + ϕ)
where, ϕ = initial phase
But given at t = 0, y(t) = +A
∴ y(0) = + A = A sin (ω × 0 + ϕ)
or $\text{sin} \phi = 1 \Rightarrow \phi = \frac{\pi }{2}$
& the desired equation is
$y \left(t\right) = A \text{sin} \left(\omega t + \frac{\pi }{2}\right)$
= A cos ωt
Putting A = 5 cm, ω = 5 rad/s
We get, y(t) = 5 sin (5t + π/2)
where, t is in second and y is in centimetre.