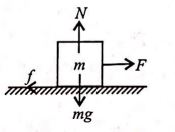
Question

A block of mass $2\, kg$ initially at rest moves under the action of an applied horizontal force of $6\, N$ on a rough horizontal surface. The coefficient of friction between block and surface is $0.1$. The work done by the applied force in $10\, s$ is (Take $g = 10\, ms^{-2}$)

• A. $200\, J$
• B. $-200\, J$
• C. $600\, J$
• D. $-600\, J$

Answer 1

Answer: (C)

The various forces acting on the block is as shown in the figure.

Here, $m = 2\, kg$, $\mu = 0.1$, $F = 6 \,N$,
$g= 10\, ms^{-2}$
Force of friction,
$f = \mu N = 0.1 \times 2\, kg \times 10\, ms^{-2} = 2\,N$
Net force with which the block moves
$F' = F - f = 6 \,N - 2\, N = 4 \,N$
Net acceleration with which the block moves
$a = \frac{F'}{m} = \frac{4\,N}{2\,kg} = 2\,ms^{-2}$
Distance travelled by the block in $10 \,s$ is
$d = \frac{1}{2}at^{2} = \frac{1}{2} \times 2\,ms^{-2}\left(10\,s\right)^{2}$
$= 100\,m\,\,\,\left(\therefore u = 0\right)$
As the applied force and displacement are in the same direction, therefore angle between the applied force and the displacement is $\theta = 0^°$.
Hence, work done by the applied force,
$W_F = Fd\, cos\theta = (6\, N)\, (100\, m) \,cos\, 0^° = 600\, J$