Question

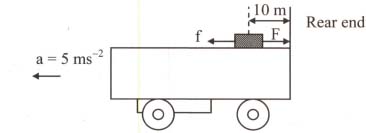
A block of mass $15\,kg$ is placed at a distance of $10\,m$ from the rear end of a long trolley as shown in figure. The coefficient of friction between the block and the surface below is $0.4.$ The trolley initally at rest is given a uniform acceleration of $5\,m/s^{2}$ . At what distance (in metres) from the starting point will the block fall-off the trolley? (Take $g=10\,m/s^{2}$ )

Answer 1

Acceleration of the block = acceleration of the trolley $=a=5\,m/s^{2}$
The force acting on the block is, $F=ma=15\times 5=75\,N$ in the backward direction. The force of limiting friction $f$ is given by, $f=\mu mg=0.4\times 15\times 10=60\,N$ in forward
direction. Hence, the net force on the block towards the right i.e., towards the rear end of the trolley is, $F^{'}=F-f=75-60=15\,N$
Acceleration due to this force is, $a^{'}=\frac{F^{'}}{m}=\frac{15}{15}=1\,m/s^{2}$
Let $t$ be the time taken for the block to fall from the rear end of the trolley travelling a distance $s=10\,m$ $s=ut+\frac{1}{2}at^{2}$
$10=0+\frac{1}{2}\times 1\times t^{2}$
$\therefore t=\sqrt{20}s$
The distance covered by the trolley in time $t=\sqrt{20}s$ is given by $s^{'}-ut+\frac{1}{2}at^{2}-0+\frac{1}{2}\times 5\times 20$
$\therefore s^{'}=50\,m$