Q.
A block of mass $100\, g$ is suspended vertically from a massless spring system of spring constant, $k=1 \,N / m$ each. The block is hit from above to impart an impulse of $2\, Ns$ . Calculate the maximum displacement from the Equilibrium position of the block. (Take, $g=10\, m / s ^{2}$ )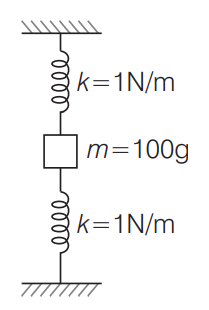
TS EAMCET 2019
Solution: