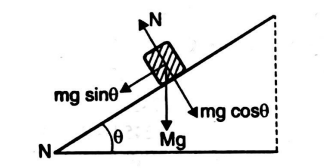
Question

A block of mass $10\, kg$ is moving up an inclined plane of inclination $ 30{}^\circ $ with an , initial speed of $5 \,m/s$. It stops after $0.5 \,s$, what is the value of coefficient of kinetic friction?

• A. 0.5
• B. 0.6
• C. $ \sqrt{3} $
• D. $ \frac{1}{\sqrt{3}} $

Answer 1

Answer: (D)

For equilibrium, normal to plane
$N=m g \cos \theta$ ... (1)
Net force along the plane downward
$F=m g \sin \dot{\theta}+f_{k}$ ...(2)
where $f_{k}$ is kinetic friction
but $f_{k}=\mu N=\mu m g \cos \theta$ ...(3)
from eq. (1), (2), and (3) we get
$\therefore \quad F=m g \sin \theta+\mu m g \cos \theta$

According to Newton's II $^{\text {nd }}$ law
$ F=m a $
$\therefore m a=m g \sin \theta+\mu m g \cos \theta $
$ \therefore $ Retardation, $ a=g \sin \theta+\mu g \cos \theta $
From equation $v=u+a t, $ we have
$ 0=u-(g \sin \theta+\mu g \cos \theta) t $
$\Rightarrow g \sin \theta+\mu g \cos \theta=\frac{u}{t} $
$ \Rightarrow 10 \times \sin 30^{\circ}+\mu \times 10 \cos 30^{\circ}=\frac{5}{0.5} $
$ \Rightarrow 10 \times \frac{1}{2}+10 \mu \times \frac{\sqrt{3}}{2}=10$
$\Rightarrow 5 \sqrt{3} \mu=5 $
or $\mu=\frac{1}{\sqrt{3}}$