Q.
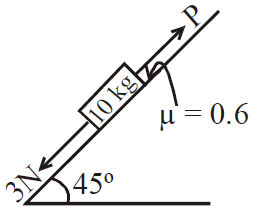
A block of mass $10\, kg$ is kept on a rough inclined plane as shown in the figure. A force of $3\, N$ is applied on the block. The coefficient of static friction between the plane and the block is $0.6$. What should be the minimum value of force $P$, such that the block doesnot move downward ?
(take $g = 10 \; ms^{-2}$)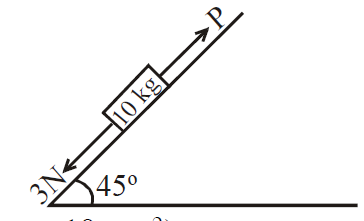
Solution:
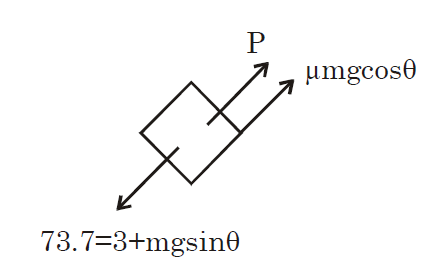
$mg \sin45^{\circ} = \frac{100}{\sqrt{2}} = 50\sqrt{2} $
$ \mu mg \cos\theta = 0.6 \times mg \times\frac{1}{\sqrt{2}} = 0.6\times50\sqrt{2} $
$ P = 31.28 \simeq 32N$