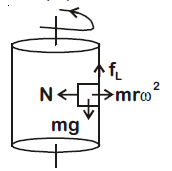
Q. A block of mass $10\, kg$ is in contact against the inner wall of a hollow cylindrical drum of radius $1\,m$. The coefficient of friction between the block and the inner wall of the cylinder is $0.1$. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be : $(g = 10m/s^2)$
Solution:
For equilibrium of the block limiting friction
$f_{L} \ge mg$
$ \Rightarrow \mu N \ge mg $
$ \Rightarrow \mu mr\omega^{2} \ge mg $
$\omega \ge \sqrt{\frac{g}{r\mu}} $
$\omega_{min } =\sqrt{\frac{g}{r\mu}} $
$\omega_{min } = \sqrt{\frac{10}{0.1 \times1}} = 10 $ rad/s