Question

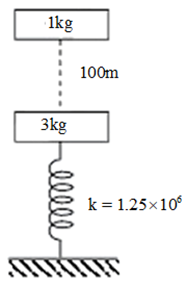
A block of mass $1 \, kg$ is dropped on a spring-mass system as shown in the figure. The block travels $100$ meters in the air before striking the $3 \, kg$ mass. Calculate maximum compression in the spring, if both the blocks move together after the collision. Spring constant of the string $k=1.25\times 10^{6}.$

• A. $2 \, cm$
• B. $4 \, cm$
• C. $8 \, cm \, $
• D. $16\,cm$

Answer 1

Answer: (A)

The velocity of $1 \, kg$ block just before striking
$V=\sqrt{2 \times 10 \times 100}=20\sqrt{5} \, ms^{- 1}$
Applying conservation of momentum, the blocks stick after the collision and move with velocity $v$
Or $1\times 20\sqrt{5}=4v$
Final velocity $ \, v=5\sqrt{5}$ ,
Using energy conservation
$KE+PE=$ const
$\frac{1}{2}\times 4\times \left(5 \sqrt{5}\right)^{2}+\frac{1}{2}k\left(\frac{3 g}{k}\right)^{2}$
$=0+\frac{1}{2}k.x^{2}$
$\therefore x^{2}=\frac{4 \times 25 \times 5}{1.25 \times 10^{6}}+\frac{30 \times 30}{\left(1.25 \times 10^{6}\right)^{2}}$
$x=\frac{20}{1000} m =2 \,cm$