Q.
A block of mass $0.24\, kg$ is attached to a spring of force constant $4\, N / m$. The coefficient of friction between the block and the floor is $0.2$. Initially the block is at rest and the spring is unstretched. An impulse is given to the block as shown in the figure. The block slides a distance of $0.18\, m$ and comes to rest for the first time. The initial velocity of the block in $m / s$ is $v =\left(\frac{ N }{100}\right)^{\frac{1}{2}}$ then, $N$ is __________. (Take $g =10\, m / s ^{2}$ )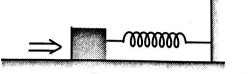
Work, Energy and Power
Solution: