Question

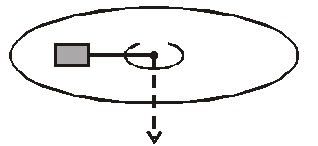
A block of mass $0.1 \, kg$ is attached to a cord passing through a hole in a horizontal frictionless horizontal surface as shown in the figure. The block is originally revolving at a distance of $0.4 \, m$ from the hole, with an angular velocity of $2 \, rad \, s^{- 1}$ . The cord is then pulled from below, shortening the radius of the circle in which the block revolves to $0.2 \, m$ . Considering the block to be point mass, calculate the new angular velocity (in $rad \, s^{- 1}$ ).

Answer 1

By conservation of angular momentum
$I_{1}\omega _{1}=I_{2}\omega _{2}$
$\Rightarrow \, \, \, MR_{1}^{2}\omega _{1}=MR_{2}^{2}\omega _{2}$
$\Rightarrow \quad \omega_2=\left(\frac{R_1}{R_2}\right)^2 \omega_1$
$=\left(\frac{0 .4}{0 .2}\right)^{2}\times 2$
$=8rad \, s^{- 1}$