Q.
A block of iron contains a hollow cavity as shown below. The block weighs $6000\,N$ in air and $4000 \,N$ in water. If the density of iron and water are $6\, g / cm ^{3}$ and $1 \,g / cm ^{3}$, then the volume of the cavity is
(Assume $g =10 \,m / s ^{2}$ )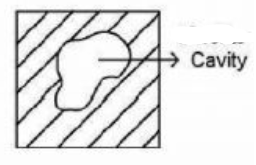
TS EAMCET 2020
Solution:
