Q. A block is moving up an inclined plane of inclination $60^{\circ} $ with velocity of $20\, m/s$ and stops after $2s$. If $g=10\,m/s^{2}$ , then the approximate value of coefficient of friction is
Delhi UMET/DPMTDelhi UMET/DPMT 2005Laws of Motion
Solution:
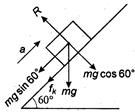
Frictional force acts in a direction opposite to direction of motion.
The various forces acting on the block are as shown.
Let a be the acceleration with which the block is moving upwards.
Then from Newtons
law, we have
$m g \sin 60^{\circ}+f=m a$ ... (i)
$R-m g \cos 60^{\circ}=0$ ... (ii)
$f_{k}=\mu R$ ... (iii)
From Eqs. (i), (ii) and (iii), we get
$m a=g\left(\sin 60^{\circ}+\mu \cos 60^{\circ}\right) m$
$m a=10\left(\frac{\sqrt{3}}{2}+\frac{\mu}{2}\right) m m a$
$=5(\mu+\sqrt{3}) m$
$\Rightarrow a=5(\mu+\sqrt{3})$
Since, block stops, hence $v =0$.
From equation of motion $v=u-a t$
$\therefore 0=u-a t$
$\Rightarrow 20=5(\sqrt{3}+\mu) \times 2$
$\Rightarrow \mu =2-\sqrt{3}$
$\Rightarrow \mu=2-1.732$
$\mu=0.27$