Question

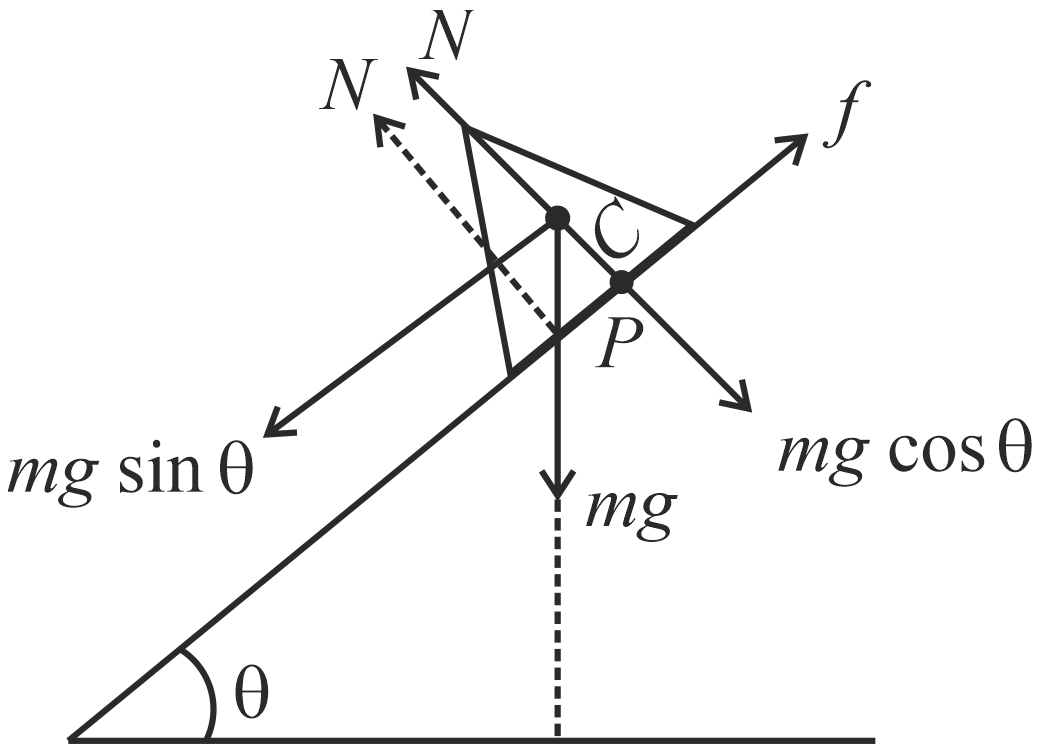
A block having equilateral triangular cross-section of side a and mass $m$ is placed on a rough inclined surface, so that it remains in equilibrium as shown in figure. The torque of normal force acting on the block about its centre of mass is:

• A. $\frac{\sqrt{3}}{2}mga \sin\theta $
• B. $\frac{1}{2 \sqrt{3}}mga \sin\theta $
• C. $\frac{1}{2 \sqrt{3}}mga \cos\theta $
• D. Zero

Answer 1

Answer: (B)

To balance the torque normal acting on the triangle shift from their original position.
From FBD, friction force $f=mg\sin\left(\theta \right)$
From FBD we can observe that torque on the center of mass is due to only friction and normal force and the body is in equilibrium. So net torque is zero.
Torque due to normal -Torque due to friction $=0$
$\Rightarrow$ Torque due to normal $=m g \sin \theta \times$$P C$
$\Rightarrow$ Torque due to normal $=m g \sin \theta \times$ $\frac{1}{2 \sqrt{3}} a$