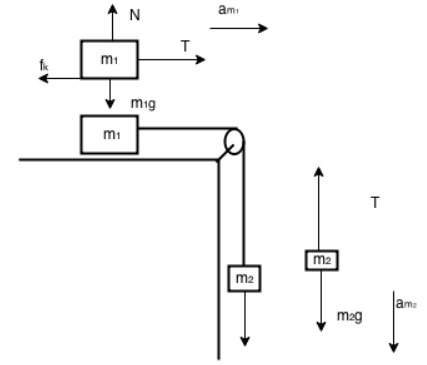
Q. A block $A$ of mass $m_1$ rests on a horizontal table. $A$ light string connected to it passes over a frictionless pully at the edge of table and from its other end another block $B$ of mass $m_2$ is suspended. The coefficient of kinetic friction between the block and the table is $\mu_k$. When the block $A$ is sliding on the table, the tension in the string is
AIPMTAIPMT 2015Laws of Motion
Solution:
The blocks $m _{1}$ and $m _{2}$ will move with combined acceleration a:
From F.B.D. of block $m_{1}$
$T - f _{1}= m _{1} a \ldots( i )$
as the block $m_{1}$ is sliding, kinetic friction will be acting:
$T -\mu_{ k } N = m _{1} a \ldots$ (ii)
$N = mg \ldots$ (iii)
From F.B.D. of block $m_{2}$
$m _{2} g - T = m _{2} a \ldots$ (iv)
adding (ii) and (iv)
$a =\frac{ m _{2} g -\mu_{ k } N }{ m _{1}+ m _{2}} \ldots( v )$
$T = m _{2} g - m _{2} a = m _{2}\left( g -\frac{ m _{2} g -\mu_{ k } N }{ m _{1}+ m _{2}}\right)$
$= m _{2}\left(\frac{ m _{1} g +\mu_{ k } m _{1} g }{ m _{1}+ m _{2}}\right)$
$= m _{1} m _{2}\left(\frac{1+\mu_{ k }}{ m _{1}+ m _{2}} g \right)$