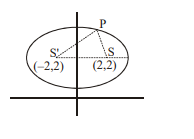
Question

A beam of light emerging from a point source have the equation $\lambda x-y+2(1+\lambda)=0, \forall \lambda \in R$, the rays of the beam strike on elliptical surface and get reflected as a beam having equation $kx - y +2(1- k )=0, \forall k \in R$. If locus of point of intersection of perpendicular tangents on ellipse is $x^2+y^2-4 y-10=0$, then

• A. eccentricity of the ellipse is $\frac{1}{3}$
• B. eccentricity of the ellipse is $\frac{2}{3}$
• C. locus of foot of perpendicular from $(2,2)$ upon any tangent to the ellipse lies on curve $x^2+y^2-4 y-5=0$
• D. locus of foot of perpendicular from $(2,2)$ upon any tangent to the ellipse lies on curve $x^2+y^2-4 y-13=0$

Answer 1

Answer: (B), (C)

Equation of PS' is
$\lambda x - y +2+2 \lambda=0$
$\Rightarrow \lambda( x +2)+(2- y )=0$
$\therefore x =-2, y =2$
focus $S^{\prime}=(-2,2)$
and PS is
$kx - y +2(1- k )=0$
$\Rightarrow k ( x -2)+(2- y )=0$
$\therefore $ focus $S =(2,2)$
$\Rightarrow 2 ae =4 \Rightarrow ae =2$
$\because\text { Director circle } $
$x ^2+( y -2)^2=14$
$\therefore a ^2+ b ^2=14 \Rightarrow a ^2+ a ^2\left(1- e ^2\right)=14 \Rightarrow a =3 $
$\text { and } b =\sqrt{5}$
$\therefore e =\frac{2}{3}$
$\therefore $ Locus of foot of perpendicular from focus is auxiliary circle
i.e. $x^2+(y-2)^2=3^2$
$\Rightarrow x^2+y^2-4 y-5=0$