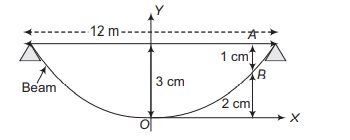
Question

A beam is supported at its ends by supports which are $12 m$ apart. Since, the load is concentrated at its centre, there is deflection of $3 cm$ at the centre and the deflected beam is in the shape of a parabola. The distance between deflection of $1 cm$ and the centre is

• A. $2 \sqrt{6} m$
• B. $3 \sqrt{6} m$
• C. $4 \sqrt{6} m$
• D. $5 \sqrt{6} m$

Answer 1

Answer: (A)

Let the vertex be at the lowest point and the axis vertical.

The equation of the parabola takes then form $x^2=4 a y$.
Since, it passes through $\left(6, \frac{3}{100}\right)$, we have $(6)^2=4 a\left(\frac{3}{100}\right)$ i.e., $a=36 \times \frac{100}{12}=300 m$.
Let $A B$ be the deflection of the beam which is $\frac{1}{100} m$.
Coordinates of $B$ are $\left(x, \frac{2}{100}\right)$.
Therefore, $ x^2=4 \times 300 \times \frac{2}{100}=24$
i.e., $ x=\sqrt{24}=2 \sqrt{6} m$