Q.
A beaker of radius $r$ is filled with water $\left(\right.$ refractive index $\left.\frac{4}{3}\right)$ up to a height $H$ as shown in the figure on the left. The beaker is kept on a horizontal table rotating with angular speed $\omega$. This makes the water surface curved so that the difference in the height of water level at the center and at the circumference of the beaker is $h ( h < < H , h < < r )$, as shown in the figure on the right. Take this surface to be approximately spherical with a radius of curvature $R$. Which of the following is/are correct? ($g$ is the acceleration due to gravity)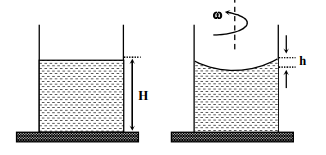
JEE AdvancedJEE Advanced 2020
Solution:
