Q.
A beaker is filled with water as shown in Fig. (a). The bottom surface of the beaker is a concave mirror of large radius of curvature and small aperture. The height of water is $h=40\, cm$. It is found that when an object is placed $4\, cm$ above the water surface, the image coincides with the object. Now the water level $h$ is reduced to zero but there will still be some water left in the concave part of the mirror as shown in Fig. (b). Find the new height (in cm) of the object $h^{\prime}$ above the new water surface so that the image again coincides with the object. (Refractive index of water $=4 / 3$ )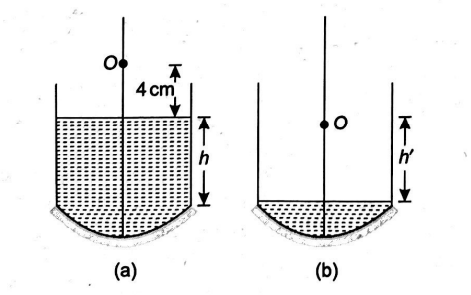
Ray Optics and Optical Instruments
Solution:
