Q.
A bead slides along a frictionless wire lying on a horizontal plane. It makes an angle of $45^{\circ}$ with $x$-axis as shown in the figure. In addition to any normal forces exerted by the wire, the bead is subject to an external force that depends on position according to formula $\vec{F}=F_{0}\left(\frac{x}{x_{0}}\right)^{2} \hat{i}+F_{0}\left(\frac{y}{y_{0}}\right)^{2} \hat{j}$. Find the work done (in $J$) by the force on the bead till it reaches the end point $P$ of the wire.
(Given: $F_{0}=1\, N , x_{0}=6\, m$, mass of bead $=2 \,kg$ )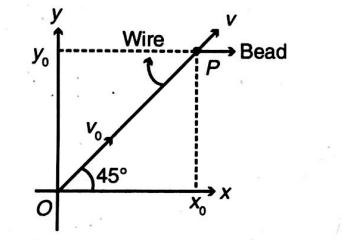
Work, Energy and Power
Solution: